Modelo estadístico para el análisis de variables negativas con aplicación a pruebas de contracción en concreto
Statistical model for analizing negative variables with application to compression test on concrete
Barra lateral del artículo
pdf
FLIP
Términos de la licencia (VER)
Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
Declaración del copyright
Los autores ceden en exclusiva a la Universidad EIA, con facultad de cesión a terceros, todos los derechos de explotación que deriven de los trabajos que sean aceptados para su publicación en la Revista EIA, así como en cualquier producto derivados de la misma y, en particular, los de reproducción, distribución, comunicación pública (incluida la puesta a disposición interactiva) y transformación (incluidas la adaptación, la modificación y, en su caso, la traducción), para todas las modalidades de explotación (a título enunciativo y no limitativo: en formato papel, electrónico, on-line, soporte informático o audiovisual, así como en cualquier otro formato, incluso con finalidad promocional o publicitaria y/o para la realización de productos derivados), para un ámbito territorial mundial y para toda la duración legal de los derechos prevista en el vigente texto difundido de la Ley de Propiedad Intelectual. Esta cesión la realizarán los autores sin derecho a ningún tipo de remuneración o indemnización.
La autorización conferida a la Revista EIA estará vigente a partir de la fecha en que se incluye en el volumen y número respectivo en el Sistema Open Journal Systems de la Revista EIA, así como en las diferentes bases e índices de datos en que se encuentra indexada la publicación.
Todos los contenidos de la Revista EIA, están publicados bajo la Licencia Creative Commons Atribución-NoComercial-NoDerivativa 4.0 Internacional
Licencia
Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-NoDerivativa 4.0 Internacional
Contenido principal del artículo
Resumen
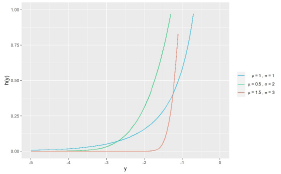
En algunas áreas de conocimiento se pueden presentar fenómenos que son representados por variables aleatorias negativas (ℝ-) ; contar con un modelo estadístico es crucial para representar esos fenómenos y explicarlos en función de otras variables auxiliares. En este trabajo se propone un modelo de regresión para el análisis de variables aleatorias negativas tomando como distribución para la variable respuesta la distribución Weibull reflejada. En este artículo reportamos el paquete RelDists creado en el lenguaje de programación R para facilitar el uso del modelo de regresión propuesto. Por medio de un estudio de simulación Monte Carlo se exploró el desempeño del proceso de estimación de parámetros. En el estudio de simulación se consideraron dos casos: sin covariables y con covariables. El primer caso se refiere a la situación en la cual sólo se tiene la variable respuesta y con ella se deben estimar los parámetros de la distribución. En el segundo caso se tiene la variable respuesta y variables explicativas que en conjunto se usan para estimar los parámetros del modelo de regresión. Adicionalmente, en el estudio de simulación se consideraron datos censurados y no censurados. Del estudio se encontró que el proceso de estimación logra estimar bien los parámetros del modelo a medida que el tamaño de la muestra aumenta y que el porcentaje de censura disminuye. En el artículo se muestra una aplicación del modelo propuesto usando datos experimentales provenientes de una prueba de contracción con probetas de concreto. En la aplicación se construyó un modelo para explicar la contracción de las probetas en función del tiempo. El modelo de regresión para variables aleatorias negativa y el paquete RelDists pueden ser usados por comunidades académicas, científicas y de negocios para el desarrollo de análisis de confiabilidad.
Descargas
Detalles del artículo
Referencias (VER)
Akaike, H. (1983). Information measures and model selection. Int Stat Inst, 44, 277–291.
Al Abbasi, J. N., Risan, H. K., & Resen, I. A. (2018). Application of Kumaraswamy Extreme Values Distributions to Earthquake Magnitudes in Iraq and Conterminous Regions. International Journal of Applied Engineering Research, 13(11), 8971–8980.
Ali, M. M., & Woo, J. (2006). Skew-symmetric reflected distributions. Soochow Journal of Mathematics, 32(2), 233–240. https://doi.org/10.1080/01966324.2008.10737716
Almalki, S. J., & Nadarajah, S. (2014). Modifications of the Weibull distribution: A review. Reliability Engineering & System Safety, 124(4), 32–55. https://doi.org/https://doi.org/10.1016/j.ress.2013.11.010
Balakrishnan, N., & Kocherlakota, S. (1985). On the double Weibull distribution: order statistics and estimation. Sankhya: The Indian Journal of Statistics, Series B, 47(2), 161–178.
Barreto-Souza, W., Santos, A. H. S., & Cordeiro, G. M. (2010). The beta generalized exponential distribution. Journal of Statistical Computation and Simulation, 80(2), 159–172. https://doi.org/10.1080/00949650802552402
Caron, R., Sinha, D., Dey, D., & Polpo, A. (2017). Categorical data analysis using a skewed Weibull regression model. In arXiv (Vol. 20, Issue 3, pp. 176–193). Multidisciplinary Digital Publishing Institute. https://doi.org/https://doi.org/10.3390/e20030176
Cohen, A. C. (1975). Multi-censored sampling in the three parameter Weibull distribution. Technometrics, 17(3), 347–351. https://doi.org/https://doi.org/10.2307/1268072
Cohen, A. C. (2016). Truncated and censored samples: theory and applications. CRC press.
Cohen, C. A., & Whitten, B. (1982). Modified maximum likelihood and modified moment estimators for the three-parameter Weibull distribution. Communications in Statistics-Theory and Methods, 11(23), 2631–2656. https://doi.org/https://doi.org/10.1080/03610928208828412
Dunn, P. K., & Smyth, G. K. (1996). Randomized quantile residuals. Journal of Computational and Graphical Statistics, 5(3), 236–244. https://doi.org/https://doi.org/10.2307/1390802
Gibbons, D. I., & Vance, L. C. (1983). Estimators for the 2-parameter Weibull distribution with progressively censored samples. IEEE Transactions on Reliability, 32(1), 95–99. https://doi.org/10.1109/TR.1983.5221484
Guure, C. B., & Ibrahim, N. A. (2012). Bayesian analysis of the survival function and failure rate of Weibull distribution with censored data. Mathematical Problems in Engineering, 2012. https://doi.org/https://doi.org/10.1155/2012/329489
Guure, C. B., & Ibrahim, N. A. (2013). Methods for estimating the 2-parameter Weibull distribution with type-I censored data. Research Journal of Applied Sciences, Engineering and Technology, 5(3), 689–694. https://doi.org/10.19026/rjaset.5.5010
Hernández, B. F., Cano, B. U., & Caicedo, E. A. C. (2021). Modelos GAMLSS para analizar el grado secado de calcio dihidratado. Revista EIA, 18(35), 1–13. https://doi.org/https://doi.org/10.24050/reia.v18i35.1439
Huang, H., Garcia, R., Huang, S.-S., Guadagnini, M., & Pilakoutas, K. (2019). A practical creep model for concrete elements under eccentric compression. Materials and Structures, 52(6), 1–18. https://doi.org/10.1617/s11527-019-1432-z
Kalsoom, U., Nasir, W., & Syed, A. (2019). On estimation of reflected Weibull distribution using bayesian analysis under informative prior. 15th Islamic Countries Conference on Statistical Sciences (ICCS-15), 49.
Kim, C., Jung, J., & Chung, Y. (2011). Bayesian estimation for the exponentiated Weibull model under Type II progressive censoring. Statistical Papers, 52(1), 53–70. https://doi.org/https://doi.org/10.1007/s00362-009-0203-2
Kim, J. S., & Yum, B.-J. (2008). Selection between Weibull and lognormal distributions: A comparative simulation study. Computational Statistics & Data Analysis, 53(2), 477–485. https://doi.org/https://doi.org/10.1016/j.csda.2008.08.012
Lai, C.-D. (2014). Generalized weibull distributions. Springer.
Lee, C., Famoye, F., & Olumolade, O. (2007). Beta-Weibull distribution: some properties and applications to censored data. Journal of Modern Applied Statistical Methods, 6(1), 173–186. https://doi.org/DOI: 10.22237/jmasm/1177992960
Meeker, W. Q., & Escobar, L. A. (2014). Statistical methods for reliability data. John Wiley & Sons.
Modarres, M., Kaminskiy, M. P., & Krivtsov, V. (2016). Reliability engineering and risk analysis: a practical guide. CRC press.
Morris, T. P., White, I. R., & Crowther, M. J. (2019). Using simulation studies to evaluate statistical methods. Statistics in Medicine, 38(11), 2074–2102. https://doi.org/https://doi.org/10.1002/sim.8086
Nagatsuka, H., Kamakura, T., & Balakrishnan, N. (2013). A consistent method of estimation for the three-parameter Weibull distribution. Computational Statistics & Data Analysis, 58(1), 210–226. https://doi.org/https://doi.org/10.1016/j.csda.2012.09.005
Nagelkerke, N. J. D. (1991). A Note on a General Definition of the Coefficient of Determination. Biometrika, 78(3), 691–692. https://doi.org/https://doi.org/10.1093/biomet/78.3.691
Odell, P. M., Anderson, K. M., & D’Agostino, R. B. (1992). Maximum likelihood estimation for interval-censored data using a Weibull-based accelerated failure time model. Biometrics, 48(3), 951–959.
Orjubin, G. (2007). Maximum field inside a reverberation chamber modeled by the generalized extreme value distribution. IEEE Transactions on Electromagnetic Compatibility, 49(1), 104–113. https://doi.org/10.1109/TEMC.2006.888172
Phadnis, M. A., Sharma, P., Thewarapperuma, N., & Chalise, P. (2020). Assessing accuracy of Weibull shape parameter estimate from historical studies for subsequent sample size calculation in clinical trials with time-to-event outcome. Contemporary Clinical Trials Communications, 17(1). https://doi.org/10.1016/j.conctc.2020.100548
R Core Team. (2021). R: A Language and Environment for Statistical Computing. https://www.r-project.org/
Regal, R. R., & Larntz, K. (1978). Likelihood methods for testing group problem solving models with censored data. Psychometrika, 43(3), 353–366. https://doi.org/https://doi.org/10.1007/BF02293645
Rigby, R. A., & Stasinopoulos, D. M. (2005). Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society: Series C (Applied Statistics), 54(3), 507–554. https://doi.org/https://doi.org/10.1111/j.1467-9876.2005.00510.x
Ross, M. S. (2012). Simulation. Elsevier.
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6(2), 461–464.
Stacy, E. W. (1962). A generalization of the gamma distribution. The Annals of Mathematical Statistics, 33(3), 1187–1192.
Stasinopoulos, M. D., Rigby, R. A., Heller, G. Z., Voudouris, V., & Bastiani, F. (2017). Flexible Regression and Smoothing Using GAMLSS in R. CRC Press.
Wei, Z., Start, M., Hamilton, J., & Luo, L. (2016). A unified framework for representing product validation testing methods and conducting reliability analysis. SAE International Journal of Materials and Manufacturing, 9(2), 303–314. https://doi.org/https://doi.org/10.4271/2016-01-0269
Xie, M., & Lai, C. D. (1996). Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function. Reliability Engineering & System Safety, 52(1), 87–93. https://doi.org/https://doi.org/10.1016/0951-8320(95)00149-2
Zhang, T., & Xie, M. (2007). Failure data analysis with extended Weibull distribution. Communications in Statistics—Simulation and Computation®, 36(3), 579–592. https://doi.org/https://doi.org/10.1080/03610910701236081